Data Structure / Algorithm - 이진 탐색 (Binary Searach)

이진 탐색

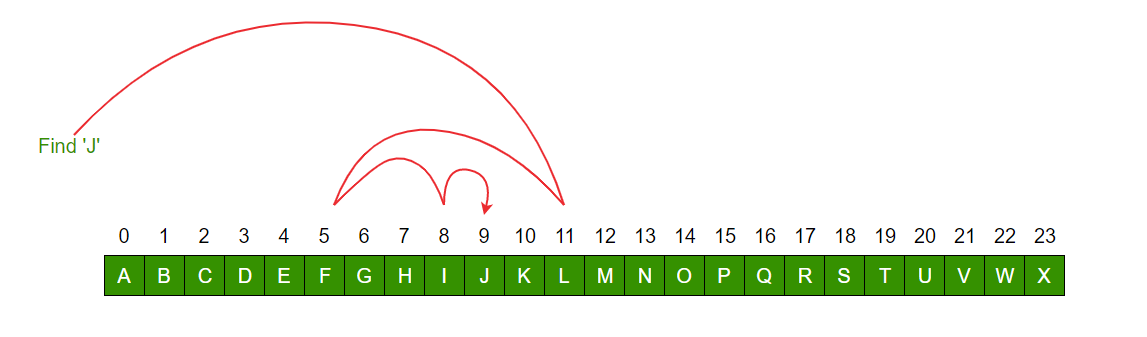이진 탐색

이진 탐색 알고리즘 (Binary Search Algorithm)은 오름차순으로 정렬된 정수의 리스트를 같은 크기의 두 부분 리스트로 나누고 필요한 부분에서만 탐색하도록 제한하여 원하는 원소를 찾는 알고리즘이다.

이진 탐색 - 나무 위키

백준 2805번 - 나무 자르기

문제 링크

출처 : https://reakwon.tistory.com/173

문제 내용

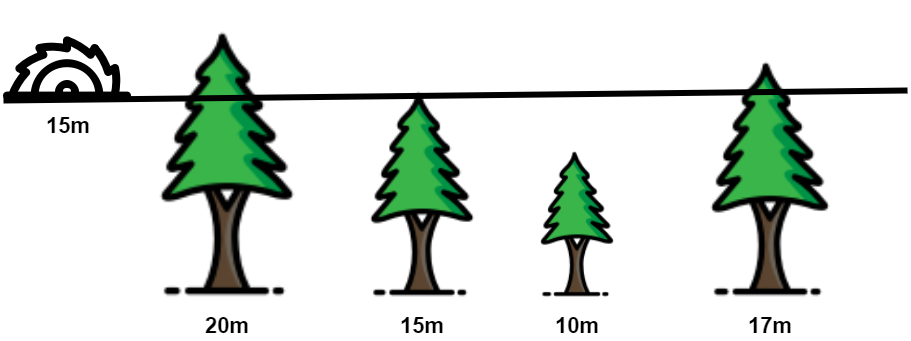
상근이는 나무 M미터를 얻기 위한 절단기로 나무를 잘라야 한다.

그 과정에서 상근이는 절단기의 높이(H)를 지정해야 한다.
그다음, 그 높이에서 나무를 모두 절단한다.
나무의 높이가 H보다 크다면 H 위의 부분이 잘릴 것이고,
낮은 나무는 잘리지 않을 것이다.

상근이는 환경을 신경 쓰기 때문에, 나무를 필요한 만큼만 가져가려고 한다.
이때, 적어도 M미터의 나무를 집에 가져가기 위한 절단기의 최대 높이를 구하는 프로그램을 작성해라.

입력 및 조건

입력 및 조건

위의 조건 속에서 시간제한은 1초인 것과,
나무의 수(N) 및 나무의 높이(M)가 (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)인 것을 고려해야 한다.

큰 수의 사용은 고려해야 할 경우가 많다는 것이므로 시간 복잡도를 생각해야 하며,
동시에 자료형을 고려해야 한다.

int의 사용은 최대 +-21억이기 때문에 오버플로우가 발생하지만
long long을 사용하면 이를 해결할 수 있다.

고민하기

이 문제를 해결하기 위해서 가장 단순하게 생각을 해보자

가장 높은 나무의 높이를 절단기의 시작 지점으로 설정한다
나무를 M미터 얻을 때까지 계속해서 절단기를 내린다

아주 단순한 풀이가 나왔다.
이를 코드로 구현하면 다음과 같다

/// Brute Force

// 절단기의 높이를 '가장 높은 나무의 높이'로 초기 설정한다
long long cuttingHeight = *std::max_element(treeHeights.begin(), treeHeights.end());
while (true)
{
  // 절단된 나무의 총길이를 구한다
  long long sumLength = 0;
  for (const auto treeHeight : treeHeights)
  {
    long long Length = treeHeight - cuttingHeight;
    if (Length > 0) sumLength += Length;
  }

  // 절단된 나무의 총길이가 충족된다면
  // 그 순간이 절단기의 최대 높이일 것이므로 종료한다
  if (sumLength >= needLength)
    break;

  cuttingHeight--;
}
// 결괏값에 절단기의 높이를 저장한다
result = cuttingHeight;

이는 Brute Force 방식으로 가장 단순하면서 무식하게 모든 경우의 수를 계산해 보는 알고리즘이다.
너무 당연하게도 시간 초과가 뜰 것이다.
왜냐하면 가져가야 하는 나무의 길이가 최대 2,000,000,000이 나올 수 있기 때문이다.

나무의 최대 높이에서 절단해 나간다면 최악의 경우는 다음과 같다

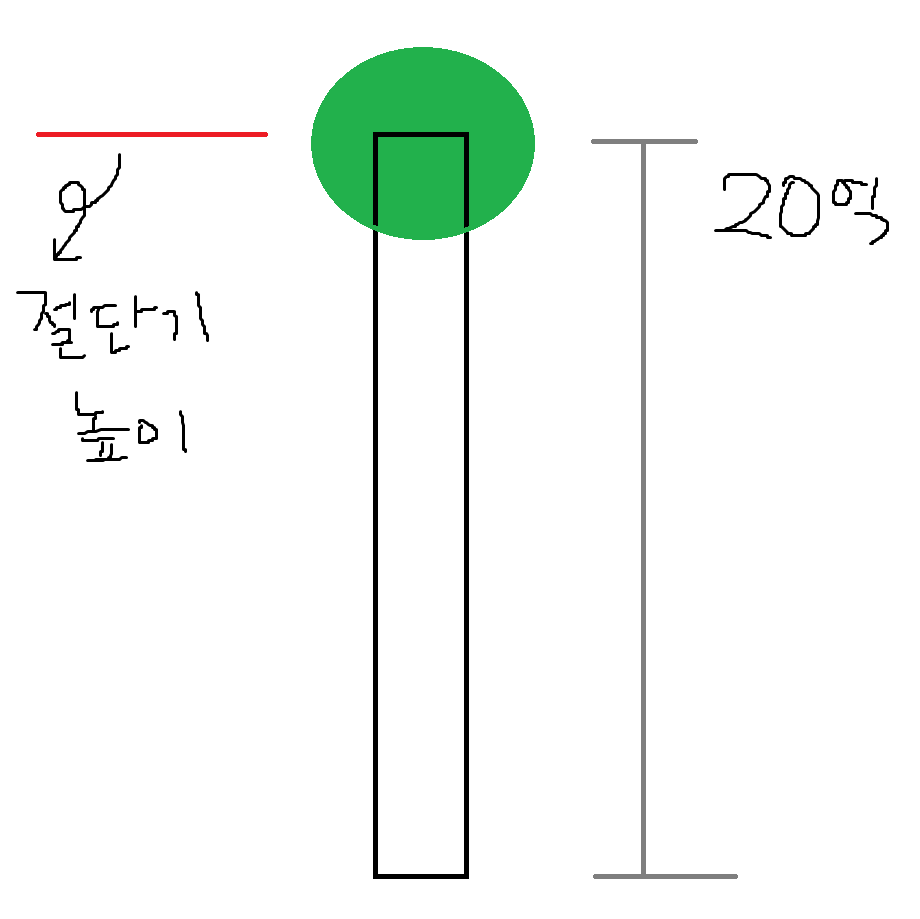최악의 경우

Brute Force 방식은 시간 초과가 발생하는 것을 확인할 수 있다

우리는 다른 방식으로 절단기의 높이를 찾아야 한다

이진 탐색을 사용

정렬된 정수의 리스트를 계속해서 절반으로 나누며 원하는 값을 찾아가는 이진 탐색을 활용한다.
이는 탐색의 시간 복잡도가 log(N)으로 매우 효율적이다.

/// Binary Search

// 이진 탐색을 위한 '정렬된 정수의 리스트'의 범위를 구한다
std::sort(treeHeights.begin(), treeHeights.end());
long long minHeight = 0;
long long maxHeight = *(treeHeights.end() - 1);

// 최대 절단기의 높이를 저장할 변수
long long maxCuttingHeight = 0;

// 이진 탐색이 얼마나 효율적인지를 보여줄 변수
int searchDepth = 0;

// 범위를 모두 이진 탐색하는 동안 반복한다
while (minHeight <= maxHeight)
{
  // 절단기의 높이를 min과 max의 중간값으로 설정
  long long cuttingHeight = (minHeight + maxHeight) / 2;

  // 절단된 나무의 총길이를 구한다
  long long sumLength = 0;
  for (const auto treeHeight : treeHeights)
  {
    long long Length = (treeHeight - cuttingHeight);
    if (Length > 0) sumLength += Length;
  }

  // 이진 탐색이 몇 번 실행되는지 계산한다
  searchDepth++;

  // 만약 딱 필요한 만큼 잘랐다면 그게 최대의 절단기 높이이므로 종료한다
  if (sumLength == needLength)
  {
    maxCuttingHeight = cuttingHeight;
    break;
  }

  // 절단된 나무가 많아서 절단기의 높이를 올려도 되는 경우
  if (sumLength > needLength)
  {
    maxCuttingHeight = cuttingHeight;
    minHeight = cuttingHeight + 1;	// ** + 1이 중요하다 **
  }
  // 절단된 나무가 부족해서 절단기의 높이를 내려야 하는 경우 (이 경우 최댓값을 갱신하지 않는다)
  else if (sumLength < needLength)
  {
    maxHeight = cuttingHeight - 1;	// ** -1이 중요하다 **
  }
}

중요 포인트

minHeight = cuttingHeight + 1;	// ** + 1이 중요하다 **
maxHeight = cuttingHeight - 1;	// ** -1이 중요하다 **

이런식으로 +1과 -1을 이용해서 범위를 조정해 주는 이유는 무한루프에 빠지지 않도록 하기 위함이다.

이 알고리즘은 while() 반복문 탈출 조건이 minHeight <= maxHeight인데
+1과 -1을 해주지 않으면 다음과 같은 상황에서 무한루프에 빠지게 된다.

예를들어,
minHeight = 10, maxHeight = 11인 경우
cuttingHeight = (minHeight + maxHeight) / 2 = 10(10.5)가 되기 때문에 무한루프에 빠지게 된다..

따라서 이진 탐색에서 적절히 탐색 범위를 좁혀줘야 한다.

이진 탐색 알고리즘으로 시간 초과를 해결

이진 탐색의 위대함

나무의 개수(N) : 1
나무의 높이(M) : 200,000,000 (2억)

이러한 상황을 가정하고 입력으로 넣어보았다.

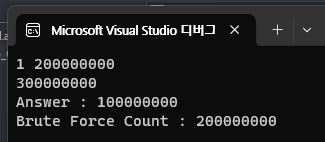Brute Force 연산 횟수

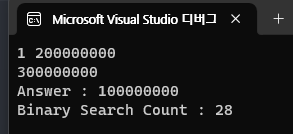이진 탐색의 연산 횟수

만약 Brute Force 알고리즘을 이용한 경우는 2억 번의 연산이 발생한다.
이진 탐색 알고리즘은 고작 28번의 연산이 발생한다.

Twitter Facebook LinkedIn

Junyeol Gong