Data Structure / Algorithm - 병합 정렬 (Merge Sort) & 퀵 정렬 (Quick Sort)

---

1. 들어가며

---

유튜버 BaaarkingDog님의 알고리즘 강의 내용을 바탕으로 한 내용입니다.

제가 푼 백준 문제는 다음과 같습니다.

1. 2751
2. 10989
3. 11931
4. 15688
5. 10814
6. 11728

일반적인 정렬 문제로
STL을 사용하면 바로 풀리는 문제이지만
STL을 사용하지 않고 직접 만든 정렬을 이용해 풀었습니다.

2. 기본 정렬 (Basic Sort)

---

2.1. 선택 정렬

2.1.1. 방식

책장에 서로 다른 높이의 무작위 배치된 책을 정렬해야 한다.
가장 먼저 떠오르는 방식이 무엇인가?

아마 대부분은 가장 짧거나 긴 것을 찾아서 끝 쪽에 배치해 가며 정렬할 것이다.

이게 ‘선택 정렬’이다.
가장 짧거나 긴 것을 ‘선택’하는 것이기 때문이다.

2.1.2. 구현

void SelectSort(vector<int>& arr, int n)
{
	// 선택 정렬 O(N^2)
	// 버블 정렬에 비해 상대적으로 교환(swap) 횟수가 적다

	for (int i = 0; i < n - 1; ++i) {
		int minIndex = i;   // 가장 작은 요소의 인덱스를 가리키는 포인터
		for (int j = i; j < n; ++j) {   // 가장 작은 요소를 찾는 범위를 j = i를 통해 줄여 나간다
			if (arr[minIndex] > arr[j]) minIndex = j;   // 이 작업은 정렬 상태와 상관없이 '상수'로 실행되는 코드이다
		}
		if (minIndex != i) swap(arr[minIndex], arr[i]);
	}
}

2.2. 버블 정렬

2.2.1. 방식

앞에서부터 인접한 두 원소를 비교하며
큰 수를 오른쪽으로 스왑하면 결국 끝까지 갔을 때는
가장 오른쪽에 제일 큰 값이 배치된다.

이게 ‘버블 정렬’이다.
인접한 두 원소가 스왑하는 방식이 ‘거품’의 이미지를 연상시키기 때문이다.

2.2.2. 구현

void BubbleSort(vector<int>& arr, int n)
{
	// 버블 정렬 O(N^2)
	// 거의 정렬된 상태라면 선택 정렬보다 빠르다

	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < n - i - 1; ++j) {
			if (arr[j] > arr[j + 1]) swap(arr[j], arr[j + 1]);  // 정렬 상태에 따라 코드 실행이 스킵될 수 있다
		}
	}
}

3. 고급 정렬 (Advanced Sort)

---

3.1. 병합 정렬

3.1.1. 방식

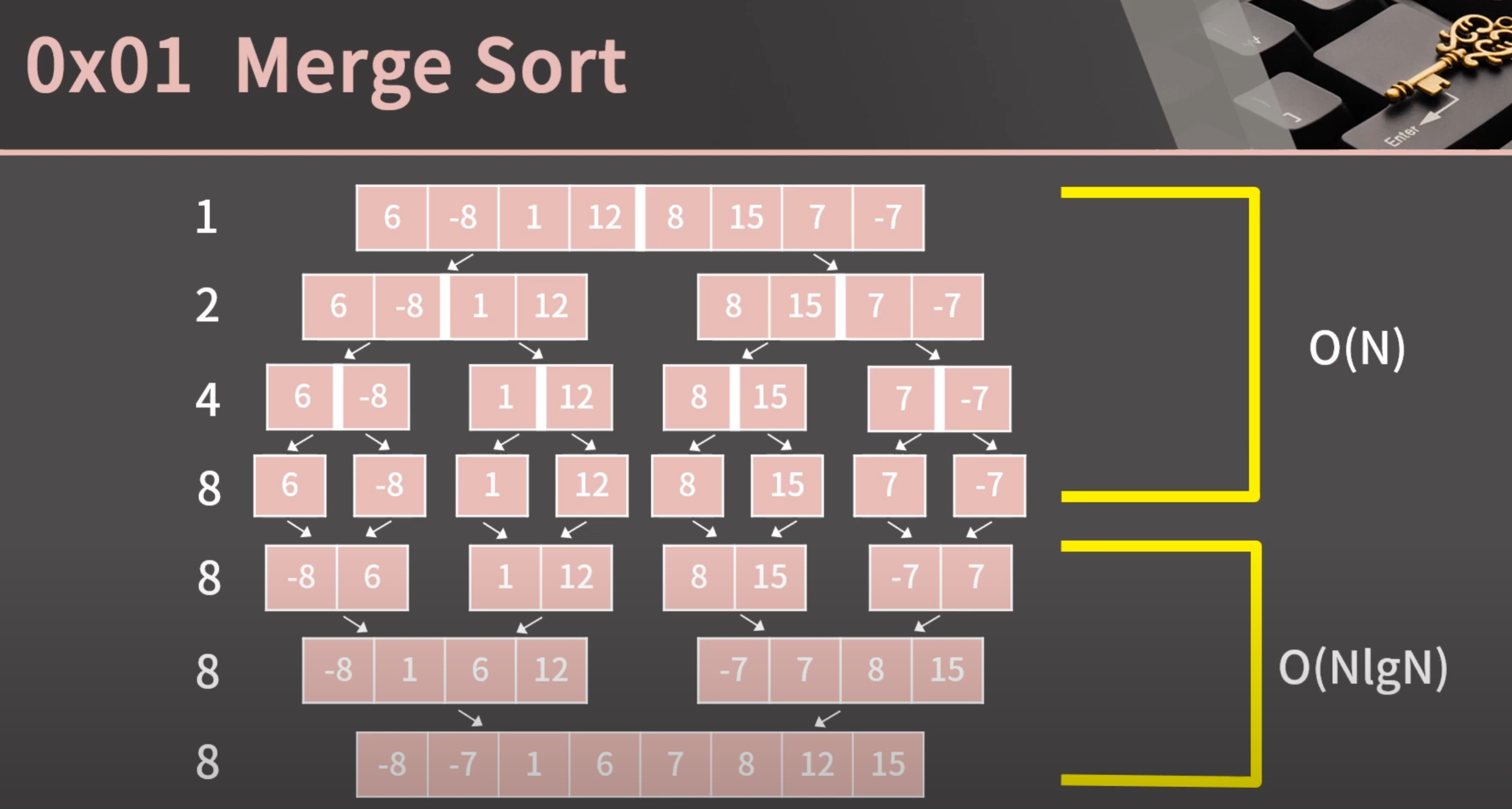병합 정렬의 분할과 병합

3.1.1.1. 분할

크기 N의 배열이 있고, 이를 크기 1까지 계속해서 이등분한다.
배열의 크기 N을 2^k개 라고 했을 때, 분할 횟수는 1 + 2 + 4 + 8 + … + 2^k가 된다.
등비수열의 합 공식에 의해 2^(k+1) - 1이 되고, 이는 곧 2N - 1 임을 말한다.
따라서 병합 정렬의 ‘분할’은 시간복잡도 O(N)이다.

3.1.1.2. 병합

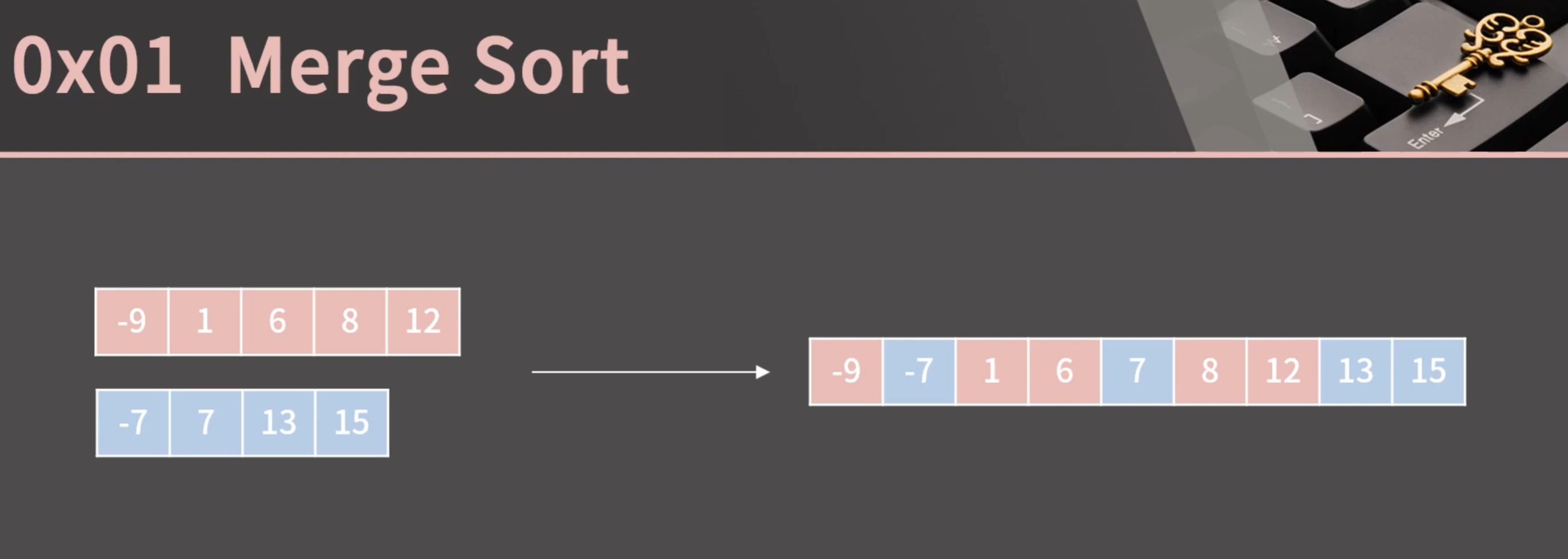정렬된 두 리스트를 하나의 정렬된 리스트로 합치기

길이가 A, B인 두 정렬된 리스트를 하나로 합치는 과정의 시간복잡도는 O(A + B)이다.

• O(1+1) + O(1+1) + O(1+1) + O(1+1) = O(8)
• O(2+2) + O(2+2) = O(8)
• O(4+4) = O(8)
• O(8)

이렇게 각 레벨에서 O(N)으로 병합하고 이는 K개가 있으므로, O(N * K) -> 즉 O(N * logN)이 된다.
따라서 병합 정렬의 ‘병합’은 시간복잡도 O(NlogN)이다.

3.1.1.3. 시간복잡도

분할과 병합 과정의 시간복잡도를 합치면
O(N) + O(NlogN) -> O(NlogN)이 된다.

3.1.2. 특성

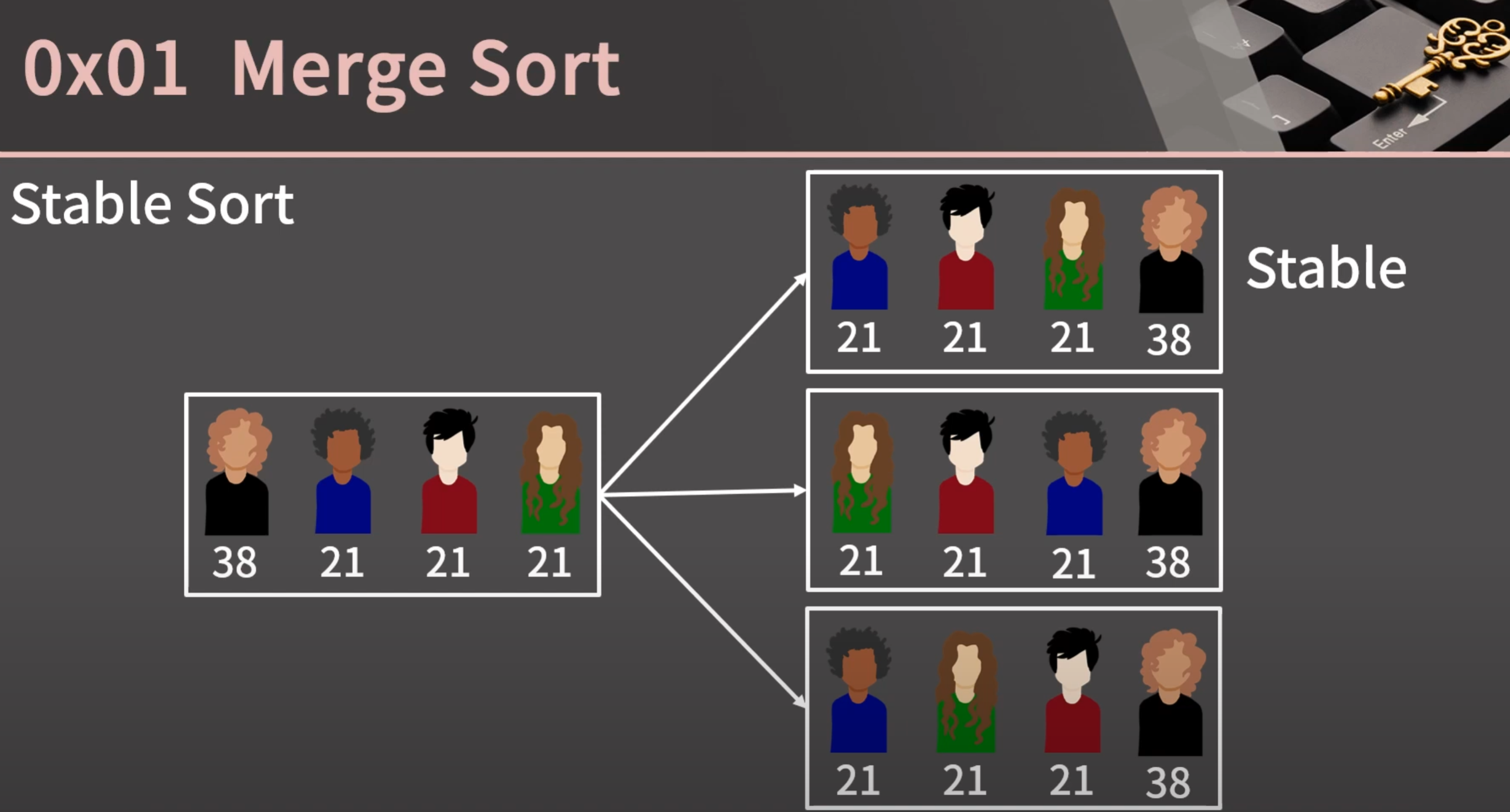Stable Sort

Stable Sort : 우선순위가 같은 원소들끼리는 입력된 데이터의 순서를 그대로 유지하며 ‘원래의 순서’를 따라가도록 하는 정렬

Stable Sort의 중요성은 특히 ‘복합 키’를 사용하여 정렬할 때 두드러진다.
예를 들어, 사람들을 이름으로 먼저 정렬하고, 그다음에 나이로 정렬하고 싶을 때,
이름으로 정렬한 순서를 유지하면서 나이로 또 정렬할 수 있다.

정렬된 두 리스트를 하나의 정렬된 리스트로 합치기

앞 리스트에서 현재 보는 원소와, 뒷 리스트에서 현재 보는 원소의 우선순위가 같을 때
앞 리스트의 원소를 먼저 보내주는 작업을 merge sort에서 자연스럽게 했기 때문에
Merge Sort는 Stable Sort라는 특성을 가진다.

Merge Sort 말고도 Bubble Sort, Insertion Sort도 Stable Sort의 종류이다.
반면 Quick Sort, Heap Sort는 UnStable Sort의 종류이다.

Stable Sort 예시

1. 파일 크기순으로 정렬하지만, ‘파일 크기’라는 우선순위가 같다면, 생성 날짜를 기준으로 정렬한다.
2. x값에 대해 우선순위가 같다면, y값에 대해 정렬한다.

Stable Sort를 사용하지 않는다면?

3.1.3. 구현

int n = 10;
int arr[1000001] = { 15, 25, 22, 357, 16, 23, -53, 12, 46, 3 };
int tmp[1000001]; // merge() 함수에서 리스트 2개를 합친 결과를 임시로 저장하고 있을 변수

void merge(int st, int en)
{
	// 하나의 정렬된 리스트로 합치는 Merge Sort의 핵심 단계
	// -> 아래와 같이 정석대로 한다면 O(N + M) = O(N)으로 할 수 있다 (선형적으로 해결이 가능하다)
    
	// cf) 버블 정렬로 한다면 O((N + M) ^ 2)

	int mid = (st + en) / 2;
	int leftIndex = st;
	int rightIndex = mid;

    // 쪼개진 두 정렬 리스트를 하나의 정렬 리스트로 합치는 것은
    // O(N)의 시간복잡도로 합칠 수 있다
	for (int i = st; i < en; ++i)
	{
		if (leftIndex >= mid) tmp[i] = arr[rightIndex++];                       // leftIndex가 꽉 찬 경우
		else if (rightIndex >= en) tmp[i] = arr[leftIndex++];                   // rightIndex가 꽉 찬 경우
		else if (arr[leftIndex] < arr[rightIndex]) tmp[i] = arr[leftIndex++];   // left의 값이 right의 값보다 작은 경우
		else tmp[i] = arr[rightIndex++];
	}

    // tmp[]에 합쳐진 리스트를 arr[]로 복사
	for (int i = st; i < en; ++i)
	{
		arr[i] = tmp[i];
	}
}

void merge_sort(int st, int en) // arr[st:en]를 정렬하고 싶다.
{
	if (st + 1 == en) return;   // 길이 1인 경우 return
	int mid = (st + en) / 2;
	merge_sort(st, mid);        // arr[st:mid]를 정렬한다.
	merge_sort(mid, en);        // arr[mid:en]를 정렬한다.
	merge(st, en);              // arr[st:mid]와 arr[mid:en]를 합친다.
}

int main()
{
	merge_sort(0, n);

    return 0;
}

3.2. 퀵 정렬

대부분의 STL은 퀵 정렬 바탕으로 만들어져 있다 (너무너무 빨라서)
하지만 STL을 사용하지 못하는 상황에서 직접 만들어 써야 할 때는 퀵 정렬 대신 병합 정렬을 사용한다

왜? -> 뒤에 나온다

3.2.1. 방식

퀵 정렬은 Pivot을 올바른 위치에 놓으면서
그 위치를 기준으로 분할 정복하는 정렬 알고리즘이다.

pivot, leftPointer, rightPointer

pivot, leftPointer, rightPointer 가 있다고 했을 때

left는 pivot 보다 큰 수가 나올 때까지 이동 (오른쪽으로)
right는 pivot 보다 작거나 같은 수가 나올 때까지 이동 (왼쪽으로)

만약 leftPointer와 rightPointer가 교차하는 경우
그 위치가 Pivot이 위치할 곳이라는 것이다

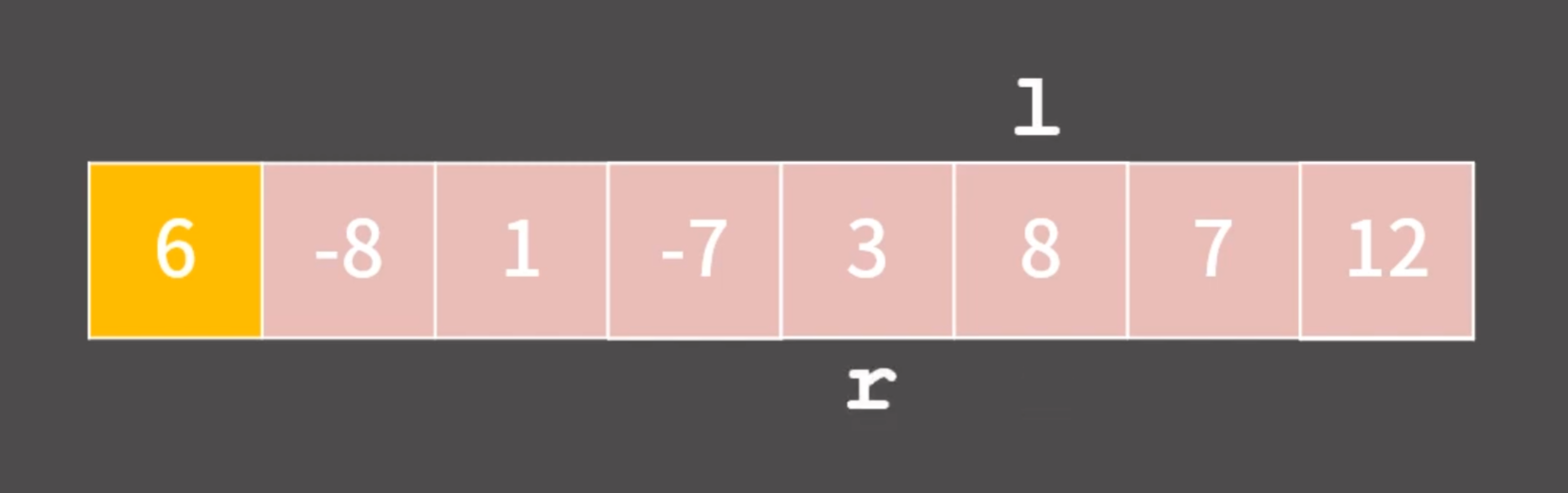leftPointer와 rightPointer가 교차하는 경우 (pivot이 위치해야 하는 곳)

왜냐하면 R Pivot L 이렇게 위치할 것인데
R 왼쪽에는 Pivot보다 작은 수, L 오른쪽에는 큰 수
이렇게 되면 Pivot이 올바르게 위치했다는 것이 자연스럽기 때문이다.

‘pivot의 왼쪽은 작은 수 오른쪽은 큰 수’ -> 여기에 주목한다

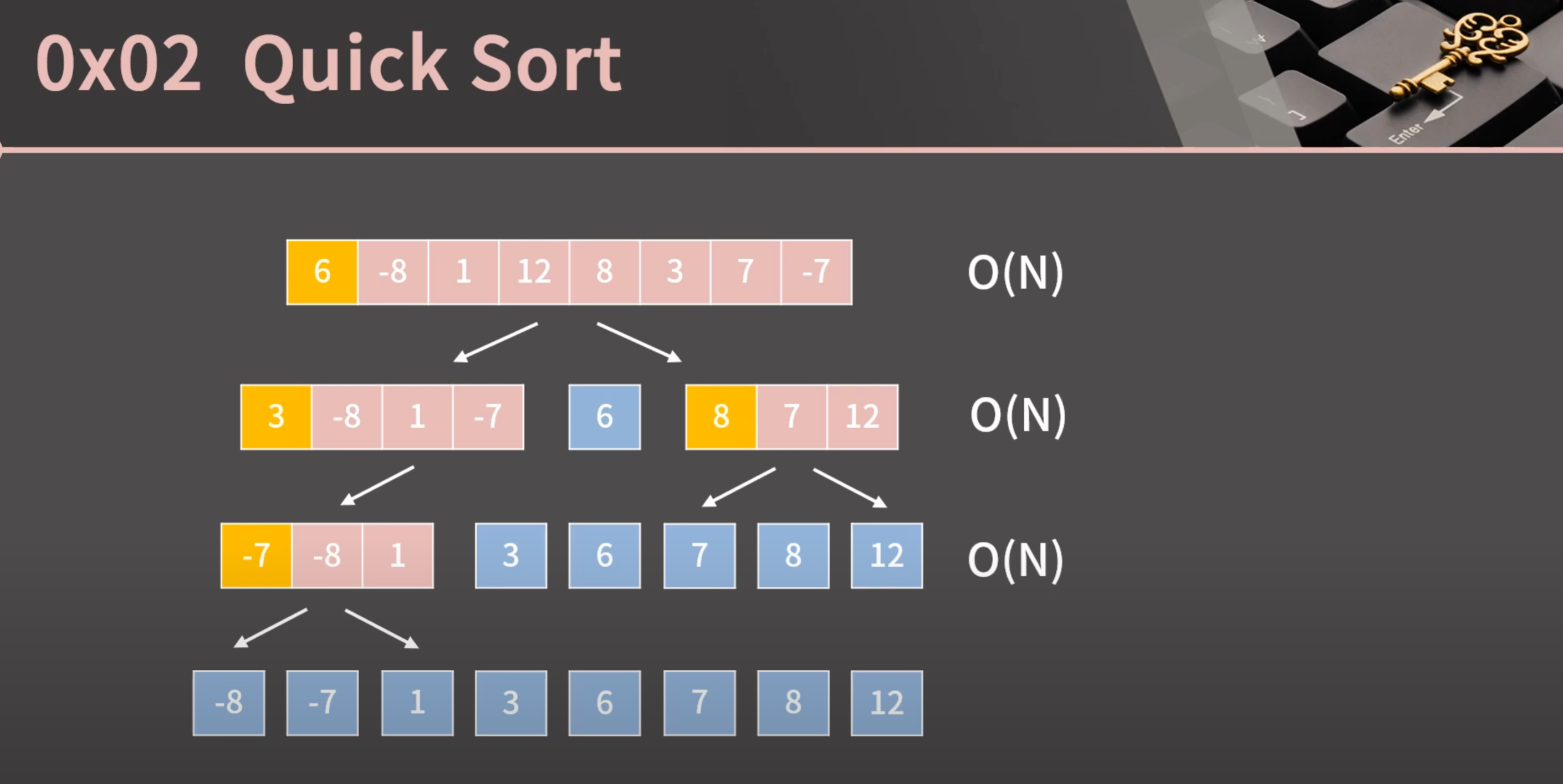퀵 정렬의 분할 과정

3.2.2. 구현

int n = 10;
int arr[1000005] = {};

// merge_sort처럼 재귀적으로 구현되는 정렬
// 매 작업마다 pivot을 제자리로 보내야 한다
void quick_sort(int st, int en)
{
	// 만약 길이가 1이하인 배열이라면 return
	if (st + 1 >= en) return;

	int pivot = st;
	int lPointer = st + 1;
	int rPointer = en - 1;

	// 피봇의 올바른 위치를 찾을 것이다
	while (true)
	{
		// ** 핵심 로직 **
		// lPointer와 rPointer을 움직이면서
		// lPointer가 rPointer의 오른쪽에 있지 않도록 하기 위해서
		// lPointer <= rPointer 조건을 추가한다
		//
		// *** 여기서 핵심은 Pointer와 Pivot의 요소의 크기를 비교하는 과정에서 하나는 등호(=)를 붙여줘야 한다는 것이다 ***
		// 
		while (arr[lPointer] < arr[pivot] && lPointer <= rPointer) lPointer++;			// lPointer 요소보다 큰 수를 찾을 때까지 오른쪽으로 이동한
		while (arr[rPointer] >= arr[pivot] && lPointer <= rPointer) rPointer--;			// rPointer 요소보다 작거나 같은 수를 찾을 때까지 왼쪽으로 이동한다

		// 만약 rPointer가 lPointer를 지나쳐서 교차하는 경우 rPointer와 pivot의 위치를 변경한다
		if (rPointer < lPointer)
		{
			// pivot의 요소의 위치를 rPointer와 교체한다
			swap(arr[pivot], arr[rPointer]);
			break;
		}

		swap(arr[lPointer], arr[rPointer]);
	}

	// 피봇을 기준으로 왼쪽 리스트와 오른쪽 리스트를 쪼갠다
	// 주의 사항 -> pivot을 포함하면 안 된다
	quick_sort(st, rPointer);
	quick_sort(rPointer + 1, en);
}

int main()
{
    quick_sort(0, n);

    return 0;
}

3.2.3. 특성

추가적인 공간(Overhead)이 필요하지 않은 In-Place Sort이다
하나의 배열 안에서의 자리바꿈만으로 정렬할 수 있기 때문이다.
따라서 tmp[] 배열을 사용하지 않고 arr[]만 사용한 것을 확인할 수 있다.

3.2.4. 주의 사항

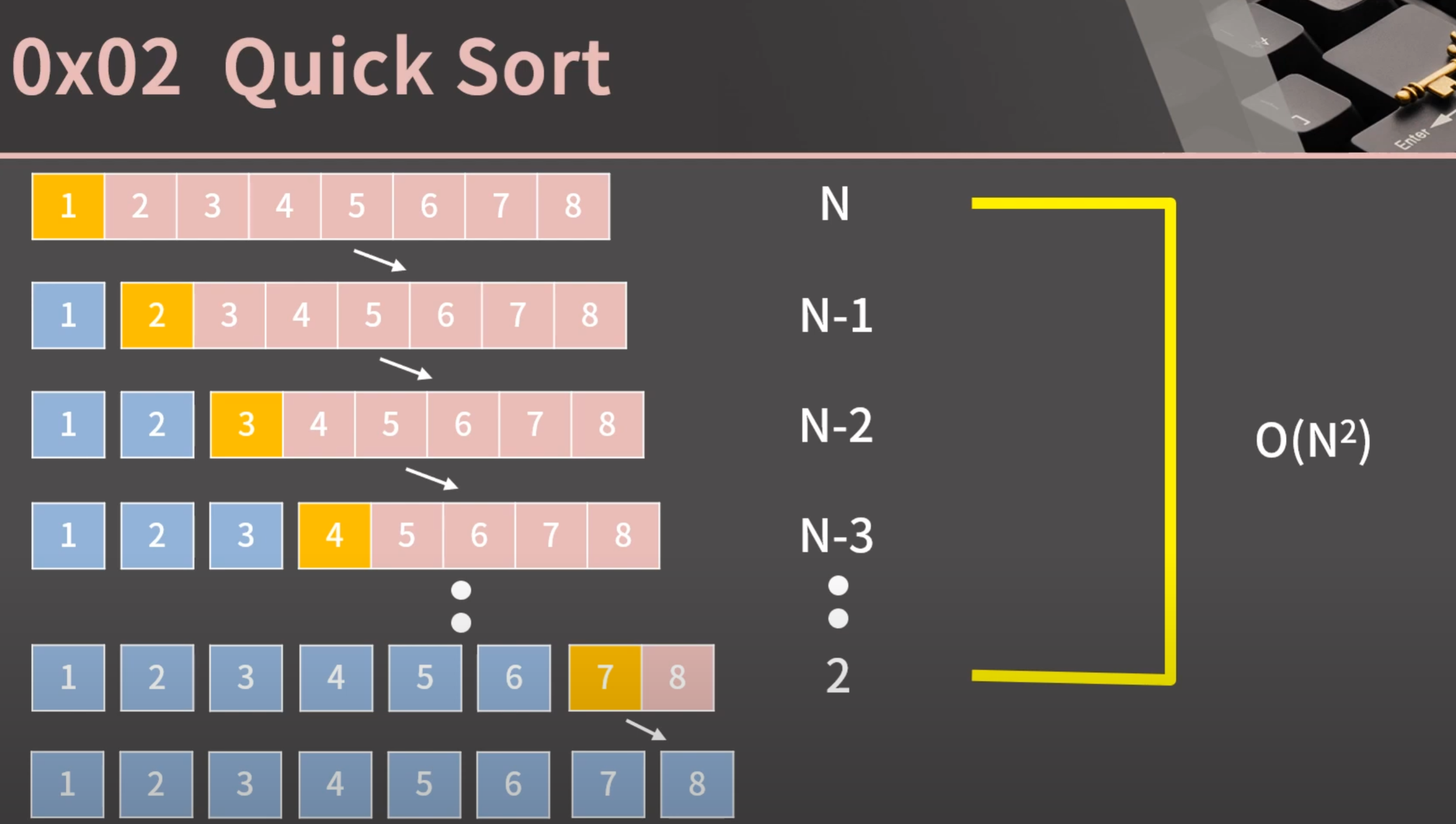최악의 경우 O(N^2)

quick sort는 평균적으로 O(NlogN)이지만, 최악의 경우 O(N^2)이 된다
예를 들어, 배열이 이미 정렬되어 있는 경우에 pivot을 항상 첫 번째 요소로 선택하면,
각 단계에서 pivot을 기준으로 배열이 분할될 때 항상 한쪽은 비어있는 배열이 되고,
다른 한 쪽은 원래 배열보다 한 요소 작은 배열이 된다.

이 경우 분할된 배열의 크기가 원래 배열의 크기보다 한 요소 작아지므로,
분할이 log n 단계를 거치더라도 모든 요소가 한 번씩만 비교되는 것이 아니라
각 단계에서 n 개의 요소가 비교되므로 총 비교 횟수는 n(n-1)/2 가 된다.

이러한 이유에서 직접 만들어 사용하는 경우에는
Quick Sort 대신 Merge Sort를 사용하라는 것이다.

Merge Sort의 경우 평균적으로 O(NlogN)이 보장되지만,
Quick Sort의 경우, 최악의 경우 O(N^2)이 되기 때문에 성능은 크게 떨어질 수 있다.

Quick Sort의 O(NlogN)과 Merge Sort의 O(NlogN)을 비교하면
Quick Sort가 더 빠르지만, Merge Sort로도 충분하기 때문에 만들어 사용할 때는
Merge Sort로 구현해 사용하자.

대부분의 STL의 경우에서 Quick Sort를 사용한다고 했는데, 정확히는 ‘최적화된 퀵 정렬’을 사용한다.
어느정도는 Quick Sort를 사용한 후 Heap Sort를 사용한다든지, Pivot을 랜덤하게 설정한다든지 등

4. Merge Sort vs Quick Sort

---

	Merge Sort	Quick Sort
시간 복잡도	O(NlogN)	최악 O(N^2) / 평균 O(NlogN) (Cash Hit Rate가 높아 평균적으로 Merge보다 빠름)
추가로 필요한 공간(Overhead)	O(N)	O(1) (pivot, left, right 이런 거 저장 - In Place Sort)
Stable Sort 여부	stable	unStable