Data Structure / Algorithm - 트리 순회 (Tree traversal)

---

다양한 자료구조

---

다양한 자료구조

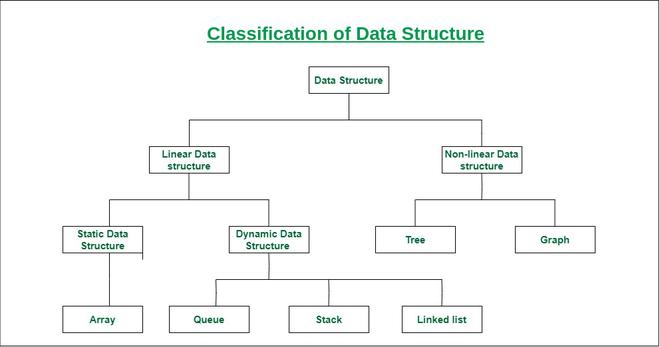
자료구조는 데이터를 효율적으로 저장하고 관리할 수 있는 방법을 제공하며, 크게 2가지로 분류할 수 있다.

1. 선형 자료구조
2. 비선형 자료구조

선형 자료구조 는 데이터가 일렬로 나열되어 있는 구조이며, 데이터 요소들이 순서를 가진다.
기본적으로 배열(Array), 연결 리스트(Linked List), 스택(Stack), 큐(Queue) 등이 있다.

비선형 자료구조 는 데이터가 계층적이거나 그래프 형태인 구조를 말한다.
이러한 구조에서 데이터 항목들 사이에서 여러 관계를 가진다.
선형 자료구조와 달리 한 요소가 두 개 이상의 요소와 관계를 가질 수 있다.
대표적으로 트리(Tree)와 그래프(Graph)가 있다.

트리 순회 (Tree traversal)

---

그중에서 트리(Tree) 자료구조의 순회(Traversal)에 대해 알아보자.

비선형 자료구조인 트리의 순회 란 트리의 모든 노드를 방문하는 과정을 뜻한다.
선형 자료구조는 순차적으로 요소에 접근하지만 비선형 자료구조는 다른 방식을 사용해야 한다.

트리 순회의 종류는 다음과 같다

• 전위 순회 (Preorder)
• 중위 순회 (Inorder)
• 후위 순회 (Postorder)

기본적으로 순회는 재귀(Recursive) 를 이용해서 쉽게 구현할 수 있다

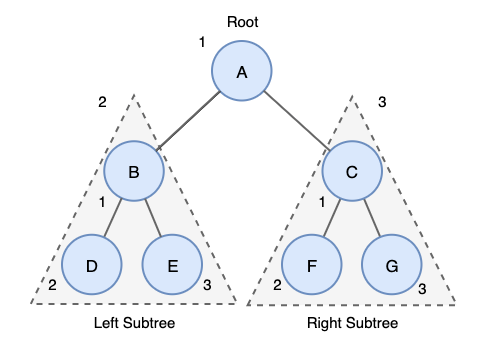
전위 순회 (Preorder)

---

전위 순회는 깊이 우선 순회(DFT, Depth First Traversal) 라고도 하며,
트리를 복사하는데 주로 사용된다.

트리를 복사할 때 전위 순회를 하는 이유는 트리 생성 시 자식 노드보다 부모 노드가 먼저 생성되어야 하기 때문이다

1. Root 노드를 방문한다
2. 왼쪽 서브 트리를 전위 순회한다
3. 오른쪽 서브 트리를 전위 순회한다

전위 순회 (출처 : https://yoongrammer.tistory.com/70)

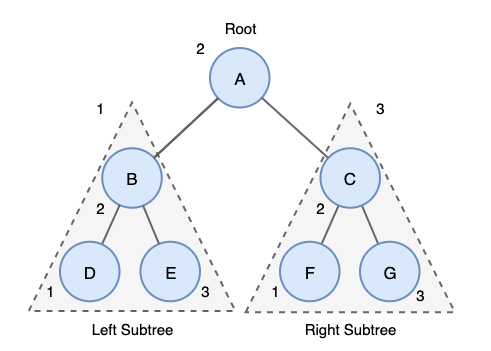
중위 순회 (Inorder)

---

중위 순회는 왼쪽 오른쪽 대칭 순서로 순회를 하기 때문에 대칭 순회(Symmetric Traversal) 라고도 하며,
이진 탐색 트리(Binary Search Tree)에서 오름차순 또는 내림차순으로 값을 가져올 때 사용된다.

1. 왼쪽 서브 트리를 중위 순회한다
2. Root 노드를 방문한다
3. 오른쪽 서브 트리를 중위 순회한다

중위 순회 (출처 : https://yoongrammer.tistory.com/70)

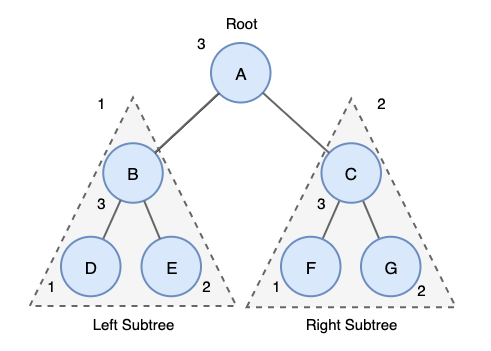
후위 순회 (Postorder)

---

후위 순회는 트리를 삭제하는데 주로 사용된다.

트리를 삭제할 때 후위 순회를 하는 이유는 부모 노드를 삭제하기 전에 자식 노드를 삭제해야 하기 때문이다

1. 왼쪽 서브 트리를 후위 순회한다
2. 오른쪽 서브 트리를 후위 순회한다
3. Root 노드를 방문한다

후위 순회 (출처 : https://yoongrammer.tistory.com/70)

코드 구현

---

#include <iostream>

struct Node
{
	// Public

	char data;

	Node* left;
	Node* right;
};

void PrintPreorder(Node* rootNode)
{
	// 루트 노드 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리

	// 입력된 노드가 유효한지 체크
	if (rootNode == nullptr)
		return;

	// 루트 노드 출력
	std::cout << rootNode->data << '\n';

	// 왼쪽 서브 트리 노드 츨력
	PrintPreorder(rootNode->left);

	// 오른쪽 서브 트리 노드 츨력
	PrintPreorder(rootNode->right);
}

void PrintInorder(Node* rootNode)
{
	// 왼쪽 서브 트리 -> 루트 노드 -> 오른쪽 서브 트리

	// 입력된 노드가 유효한지 체크
	if (rootNode == nullptr)
		return;

	// 왼쪽 서브 트리 노드 츨력
	PrintInorder(rootNode->left);

	// 루트 노드 출력
	std::cout << rootNode->data << '\n';

	// 오른쪽 서브 트리 노드 츨력
	PrintInorder(rootNode->right);
}

void PrintPostorder(Node* rootNode)
{
	// 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 노드

	// 입력된 노드가 유효한지 체크
	if (rootNode == nullptr)
		return;

	// 왼쪽 서브 트리 노드 츨력
	PrintPostorder(rootNode->left);

	// 오른쪽 서브 트리 노드 츨력
	PrintPostorder(rootNode->right);

	// 루트 노드 출력
	std::cout << rootNode->data << '\n';
}

void Padding()
{
	std::cout << "===========================" << '\n';
}

int main()
{
	// 노드 초기화
	const int nodeCount = 7;
	Node nodes[nodeCount + 1];
	for (int i = 1; i <= nodeCount; ++i)
	{
		nodes[i].data = i + '@';	// '@' = 64 (ASCII)
		nodes[i].left = nullptr;
		nodes[i].right = nullptr;
	}

	// 노드 연결
	nodes[1].left = &nodes[2];
	nodes[1].right = &nodes[3];
	nodes[2].left = &nodes[4];
	nodes[2].right = &nodes[5];
	nodes[3].left = &nodes[6];
	nodes[3].right = &nodes[7];

	Node* rootNode = &nodes[1];

	// 전위 순회 실행
	PrintPreorder(rootNode);

		Padding();

	// 중위 순회 실행
	PrintInorder(rootNode);

		Padding();

	// 후위 순회 실행
	PrintPostorder(rootNode);

	return 0;
}