Programming - 1.1 + 0.1 == 1.2는 거짓일 수 있다

---

1.1 + 0.1 == 1.2는 true ? false ?

---

    cout << (1.1f + 0.1f == 1.1f) << endl;

    // output
    // false

이유가 뭘까? 분명 우리가 수학을 할 때 1.1 + 0.1을 계산하면 1.2가 나올텐데 말이다.
이유는 컴퓨터가 실수형 자료형을 메모리에 저장하는 방식에 있다.

컴퓨터가 실수형 자료를 다루는 방법

---

실수 자료형 float는 IEEE 754 32bit(4byte) 부동 소수점 표준에 따라 특별한 방식으로 RAM에 저장된다.
크기의 float는 부호 비트, 지수 부분, 가수 부분으로 나뉘는데 다음 그림과 같다.

32bit 크기의 float와 64bit 크기의 double 자료형의 구조

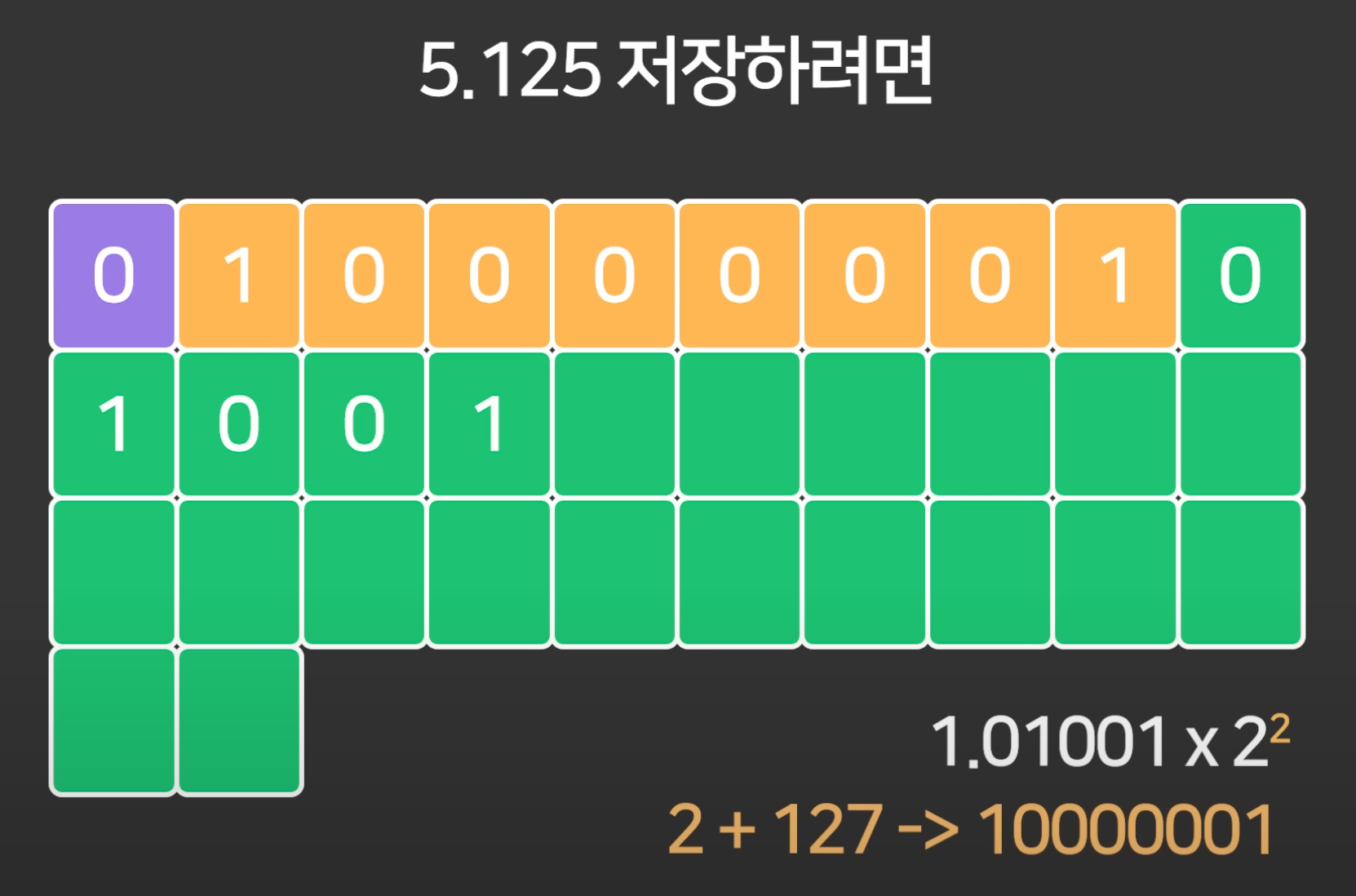
예를들어 float a = 5.125라는 변수는 다음과 같은 변환을 거쳐 메모리에 저장된다.

1. 정수부 / 소수부를 각각 2진수로 변환해 합친다.
   -> 정수부 : 5(10)
   => 101(2)

   -> 소수부 : 0.125(10)
   => 0.25(10) => 0.5(10) => 1.0(10) => 001(2)

   -> 101.001(2) = 1.01001 x 2^2(2)

2. 부호, 지수, 가수 부분으로 나눠 메모리에 저장한다.
   -> 부호 비트 (1 비트): 0 (+), 1 (-)

   -> 지수 부분 (8 비트): 지수 값은 127에 Exponent을 더한 값으로 표현
   => 127 + 2 = 129이므로 10000001(2)

   -> 가수 부분 (23 비트): 왼쪽부터 Mantissa의 값을 채워넣음

실수 자료형의 부동소수점 구조

이렇게 하면 컴퓨터가 부동 소수점을 메모리에 저장할 수 있게 된다.

출처 : (https://www.youtube.com/watch?v=-GsrYvZoAdA)

이런식으로 정해진 공간 안에 내가 저장하려는 값이 모두 다 들어가면 실수형 계산을 하는 데에도 문제가 없다.

출처 : (https://www.youtube.com/watch?v=-GsrYvZoAdA)

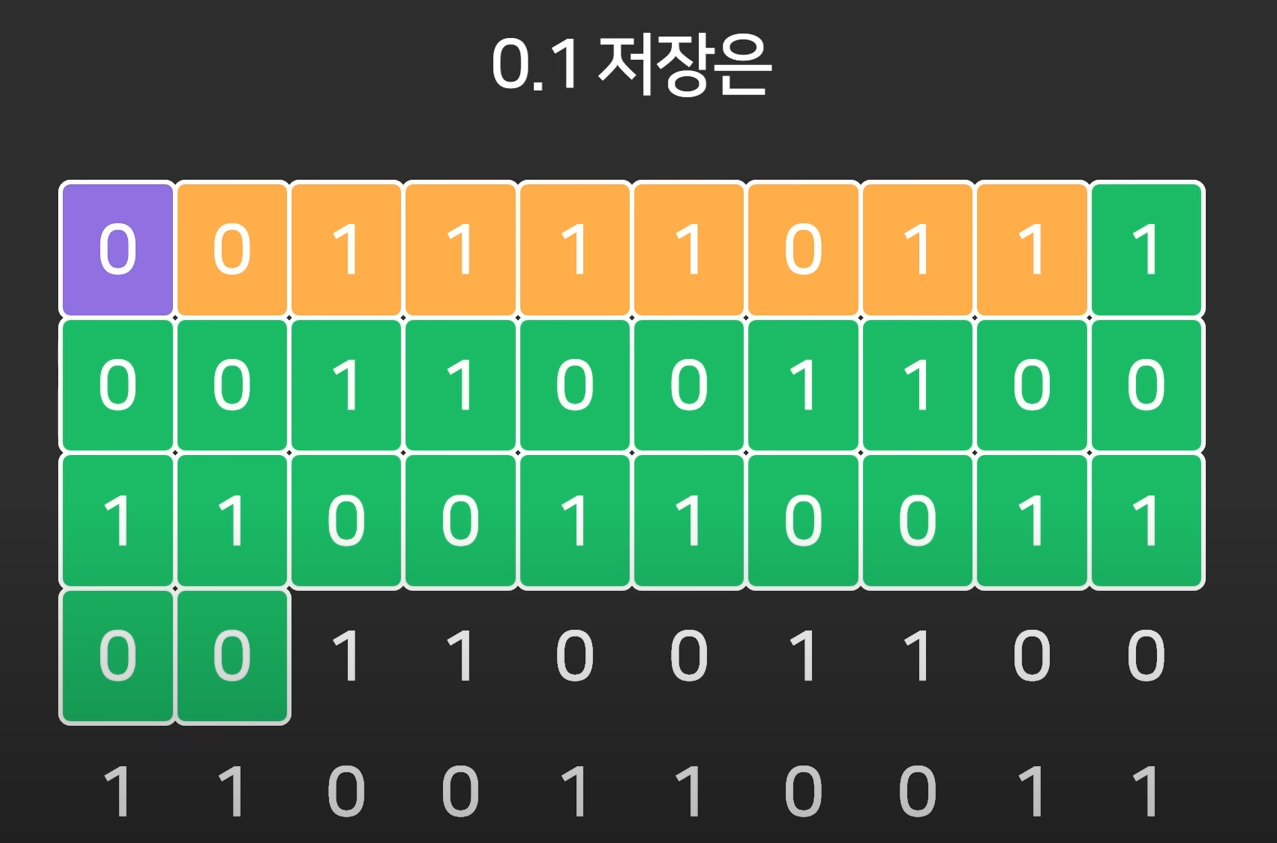
하지만 이런식으로 0.1을 이진수로 변환하는 과정에서 무한소수가 나온다면..?
메모리에 들어오지 못하는 수들은 버려지게 될 것이고, 결국 오차가 발생하게 된다.

이러한 이유로 1.1f + 0.1f의 값이 1.2f와 같을 수 없게 되는것이다.

활용

---

위의 내용을 완전히 이해했다면 아래의 결과 또한 이해될 것이다.

    // 가수 부분이 넘치지 않고 값이 모두 들어오기 때문에 실수형이라 할지라도 오차가 발생하지 않는다.
    cout << (0.125f + 0.125f == 0.25f) << endl;

    // output
    // true

    // float에 비해 오차가 훨씬 적은 double 자료형을 사용하면 true가 출력된다.
    cout << (1.1 + 0.2 == 1.3) << endl;

    // output
    // true